| Kirchhoff's Voltage Law (KVL) |
|
|
In any closed electrical circuit or mesh, the algebraic sum of all the electromotive forces (e.m.fs) and voltage drops in resistors is equal to zero.
|
|
i.e in any closed circuit or mesh,
Algebraic sum of e.m.fs + algebraic sum of voltage drops = 0
|
|
 |
|
|
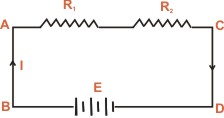
The validity of Kirchhoff's voltage law can be easily established
by referring to the loop ABCDA as shown in diagram. If we start
from any point (say point A) in this closed circuit and go back
to this point (i.e. point A) after going round the circuit then
there is no increase or decrease in potential. This means that
algebraic sum of the e.m.fs of all the sources (here only one
e.m.f source is considered) met on the way plus the algebraic
sum of the voltage drops in the resistances must be zero. |
|
|
Kirchhoff's voltage law is based on the law of conservation
of energy. i.e. net change in the energy of a charge after completing
the closed path is zero. |