| Malus's Law |
|
|
According to malus, when completely plane polarized light is incident on the analyzer, the intensity I of the light transmitted by the analyzer is directly proportional to the square of the cosine of angle between the transmission axes of the analyzer and the polarizer. |
|
|
i.e I ∞ cos2θ |
|
 |
|
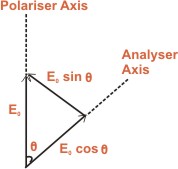
Suppose the angle between the transmission axes of the analyzer and the polarizer is θ. The completely plane polarized light form the polarizer is incident on the analyzer. If E0 is the amplitude of the electric vector transmitted by the polarizer, then intensity I0 of the light incident on the analyzer is
I ∞ E02
|
|
|
The electric field vector E0 can be resolved into
two rectangular components i.e E0 cosθ and E0
sinθ. The analyzer will transmit only the component ( i.e
E0 cosθ ) which is parallel to its transmission
axis. However, the component E0sinθ will be absorbed by the analyser.
Therefore, the intensity I of light transmitted
by the analyzer is, |
|
|
I ∞ ( E0 x cosθ )2
|
|
|
I / I0 = ( E0 x cosθ )2 / E02 = cos2θ |
|
|
I = I0 x cos2θ
|
|
|
Therefore, I ∞ cos2θ. This proves law of malus.
|
|
|
When θ = 0° ( or 180° ), I = I0 cos20°
= I0 That is the intensity of light transmitted by
the analyzer is maximum when the transmission axes of the analyzer
and the polarizer are parallel. |
|
|
When θ = 90°, I = I0 cos290° = 0
That is the intensity of light transmitted by the analyzer is minimum when the transmission axes of the analyzer and polarizer are perpendicular to each other.
|